как завязать, простая и понятная схема
Академический узел также называют академическим морским узлом, так как он часто применяется в морской и туристической сфере.
История узла
Данный узел имеет длинную историю и, как уточнялось, является модификацией хирургического. А этот в свою очередь появился благодаря классическому прямому узлу.
Как выглядит узел?
Узел является соединяющим и имеет несколько отличий от хирургического узла, что и делает его надежнее. Выглядит он как два полуузла, которые завязываются последовательно один над другим в разных направлениях. В обеих петлях присутствуют два переплетения, поэтому узел часто называют параллельным.
Где применяется узел?
Основная функция академического узла – связывание (соединение) веревок и тросов. Благодаря этому можно с легкостью перевязать коробку или тюк, чтобы надежнее зафиксировать ее нахождение.
Углубляясь в туристическую сферу, данный узел применяется для стягивания веревок и тросов между собой, даже если они разного диаметра.
Важно! Узел будет держаться надежнее, если веревки, которые необходимо связать, находятся под напряжением.
Применяют академический узел и в рыбалке, поэтому вязать академический узел можно не только на веревках из растительных материалов, но и синтетических тросах, лесках и мононитях.
Внимание! На мононити шансы развязывания узла увеличиваются.
Кроме этого, еще одной сферой использования узла является хирургия и альпинизм.
Преимущества и недостатки узла
Поскольку данный узел является улучшенной версией хирургического узла, то он более надежен и прочен. Если веревки находятся под напряжением, то шансы его развязывания равны нулю. Главной чертой узла является то, что он вообще не может развязываться.
Академический узел легко завязывается и затем развязывается при необходимости. Когда узел при натяжении прочно затягивается, его намного проще развязать, чем хирургический.
К недостаткам отнесем то, что он не компактен и развязывается на мононитях и лесках.
Как вязать академический узел?
Существует несколько способов завязать академический узел, но следующая схема является наиболее распространенной и надежной. Несмотря на то, что техника его вязания усложняется по сравнению с хирургическим и прямым узлом, он все равно вяжется легче.
Для вязания узла нам понадобится две веревки разного диаметра. Следуйте поэтапно, чтобы прийти к успеху:
1. Положите веревки параллельно друг другу перед собой.
2. Сделайте петлю из веревки большего диаметра.
3. Просуньте веревку меньшего диаметра в эту петлю.
4. Затем оберните ее конец вокруг петли.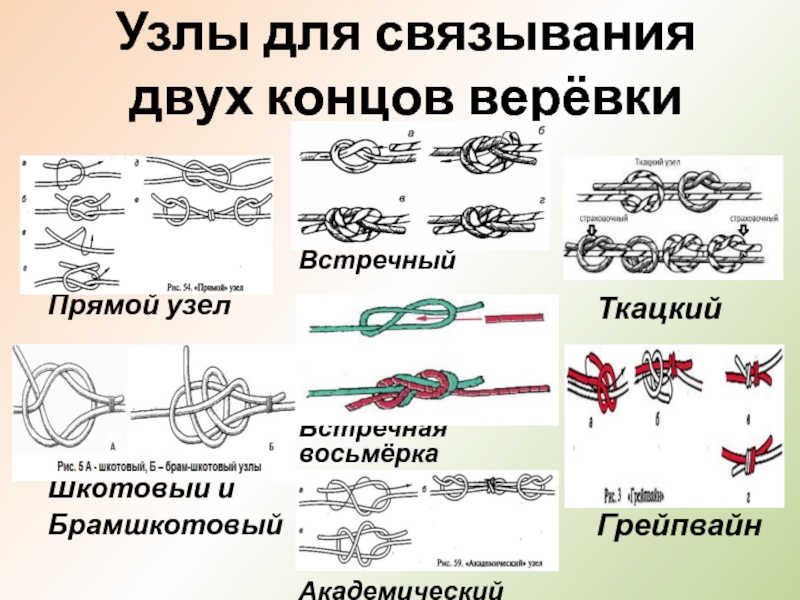
5. Конец веревки меньшего диаметра снова просуньте в петлю.
6. У вас получится такая конструкция из двух веревок разного диаметра. Затяните их и узел готов.
Попрактиковавшись в вязании академического узла, можете смело применять его при любой ситуации. А мы напоминаем, что вязать узлы различной сложности – настоящее искусство.
Академический узел
Узел Академии — это походный узел, используемый для связывания двух лесок, веревок, линий или шнуров. Это соединение двух кусков нити в две петли (два полуузла), которые параллельны друг другу. Нити всегда должны быть направлены в противоположную сторону друг от друга, иначе прочность узла снижается.
Читайте также: Узел Рапала
В этой статье вы найдете пошаговые инструкции о том, как завязать академический узел, а также узнаете, для каких целей он годится, а для каких нет.
Назначение академического узла
Академический узел используется в основном для:
- завязывание веревок в походах;
- используется в медицине и чаще всего в этой области называется двойным академическим узлом;
- В рыболовстве для соединения веревок или шнуров разного диаметра;
Преимущества
- Хорошо держится на веревках, толстых шнурах, несглаженной рыболовной тесьме.
- Его можно вязать двумя способами.
- Его можно усложнить и усилить, добавив витки. Подходит для тонких линий и плетеных шнуров.
- Подходит для связывания двух веревок, концы которых чем-то заняты (не требует, чтобы при завязывании вся длина веревки проходила через узел).
Недостатки
- Хотя запомнить, как завязать узел, легко, завязывание узла на практике отнимает много времени. Кроме того, если вы связываете 2 отрезка лески одного цвета (или 2 шнура), необходимо следить за концами и не перепутать их. В противном случае, когда вы попытаетесь растянуть узел, он может развязаться.
- Он плохо держится на флюорокарбоне или жесткой мононити. Blood Knot и Uni Knot являются лучшими заменителями.
Пошаговая инструкция по вязанию
Вот 2 пошаговые схемы завязывания академического узла.
Первый вариант более трудоемкий и хорошо работает, если один из шнуров (желтый в примере ниже) совершенно негибкий и не подходит для обматывания вокруг другого шнура.
На рыбалке я рекомендую использовать второй вариант. Хотя конечный результат точно такой же.
Первый способ
Шаг 1: Сложите толстую веревку или струну пополам. Это желтый шнур на фотографии.
В предыдущей статье вы можете прочитать: Скользящий узел – что это такое, и как его завязывать
Шаг 2: Начните оплетать второй шнур, начиная с конца петли первого шнура с изнанки. Сделайте 3 полные косы.
Шаг 3: Далее слегка вытяните шнур №2, чтобы у вас было достаточно места для того, чтобы сделать еще несколько витков уже вокруг нижней части шнура №1 (желтый шнур). Сделайте 3 полных оборота. Оранжевый шнур должен выходить из узла с внутренней стороны, как показано на рисунке. Верхняя и нижняя косы должны зеркально отражать друг друга. Это важно для поддержания прочности академического узла.
Шаг 4: Увлажните узел (если у вас тесьма или леска) и хорошо затяните его, потянув за все 4 секции (сильнее потяните за верхние секции).
Смачивание важно для того, чтобы леска не прогорела и не деформировалась при сильном затягивании.
Шаг 5: Равномерно затяните узел, прилагая большее усилие только к верхним концам шнура. После полной затяжки окончательно затяните нижние звенья, так как они были соединены этим узлом. Верхние части можно отрезать плоскогубцами или ножницами на расстоянии не менее 1 мм от узла. Если вы используете веревки или шнуры толщиной более 0,3 мм, оставьте больший запас, чтобы предотвратить растяжение и распутывание узла под нагрузкой.
Второй способ
Шаг 1: Вот 2 куска лески или бечевки, которые вы хотите связать вместе.
Шаг 2 Переплетите их друг с другом 2 раза. Чем тоньше линия, тем больше поворотов нужно сделать. В показанном случае одна линия оборачивается вокруг другой на 2 полных оборота. Попробуйте 3 оборота, если линия меньше 0,15 мм, и 4 оборота, если линия меньше 0,1 мм.
Шаг 3: Потяните сильнее за два конца лески, чтобы сделать еще одну итерацию поворотов. Начинайте делать новые повороты с линиями вокруг себя, чтобы косы отскакивали друг от друга. На фотографии ниже видно, что оранжевый шнур с правой стороны узла как снизу, так и сверху обхватывает желтый шнур снаружи. С левой стороны, наоборот, изнутри в обоих случаях. Сделайте то же самое, иначе прочность узла снизится.
Шаг 4: Затяните узел, предварительно смочив его в воде в случае тонкой лески и плетеной лески. Равномерно потяните за все концы лески. Отрезайте лишние концы плоскогубцами или ножницами только тогда, когда вы убедитесь, что правильно затянули узел, как на верхних участках лески, так и на основных нижних участках, которые вы завязываете этим узлом.
Вы шаг за шагом научились завязывать академический узел двумя способами. Вы проработали преимущества и избежали ошибок, чтобы избежать ослабления узла.
Искусство и магия тривиального узла
2119 слов | 10 минут
Поделиться этим контентом
Наука
Математика
Одно из моих самых больших разочарований при поливе сада заключается в том, что шланг всегда кажется завязанным узлом. Независимо от того, насколько аккуратно я сворачиваю его, узлы появляются везде, где они вам не нужны — на садовых шлангах, проводах наушников, удлинителях или даже на ваших мышцах. Однако в большинстве случаев эти узлы — всего лишь иллюзия, а мой шланг — всего лишь сложный «узел», как сказали бы математики.
Математики очень подробно изучают узлы. Не для того, чтобы их садовые шланги не запутались, а для того, чтобы лучше понять реальность. Например, этот раздел математики дает представление о структуре ДНК и запутанности в квантовой механике и о поведении жидкостей. Но узлы сами по себе могут быть красивыми и увлекательными объектами изучения.
Развязанный узел, также известный как тривиальный узел, является самым простым узлом. В своей простейшей форме это просто цикл, но со скрытой сложностью. Развязка обманчива, потому что то, что выглядит как узел, на самом деле таковым не является. Математики разработали сложные узлы для изучения их свойств. Незавязанный узел также вдохновлял художников как произведения искусства. Наконец, фокусники разработали методы создания узлов, которые выглядят как настоящие узлы.
Эта статья — ода тривиальному узлу и содержит галерею математических, художественных и магических диаграмм незавязанных узлов.
Проблема развязывания
Теория узлов — молодой раздел математики, зародившийся около века назад.
Незавязанный узел — это замкнутая петля, которая не завязана узлом. Это запутанный способ сказать, что узел — это круг. Хотя это описание максимально простое, не всегда понятно, завязана петля или просто кольцо. На диаграмме ниже показаны два примера, которые бесспорно не завязаны.
Две простые проекции узла. Одной из фундаментальных и наиболее сложных задач теории узлов является задача о развязывании узлов.0046 . В то время как в физическом мире вы просто дергаете за нитку, чтобы проверить ее узел, нам требуется более строгий и воспроизводимый процесс в абстрактном мире математики.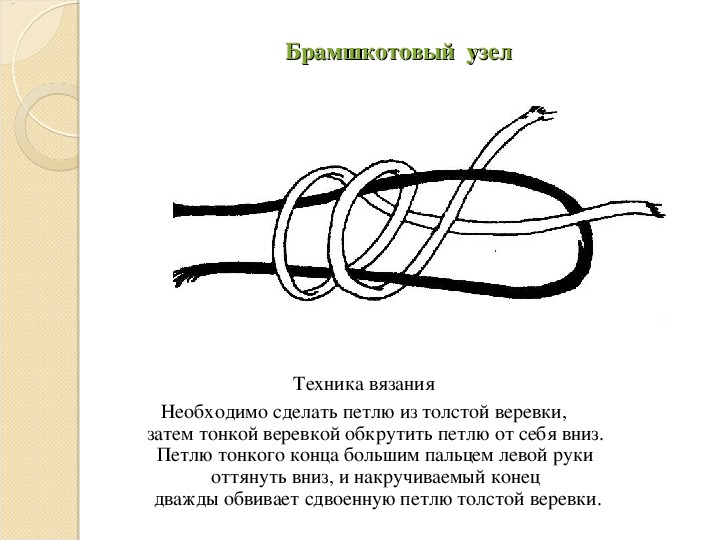
Пример ниже выглядит как настоящий узел, но вы увидите, что это просто петля, когда вы создадите ее из куска веревки.
Проблема развязывания обманчива, потому что сложные проекции развязывания выглядят как настоящие узлы. Математики разработали множество систематических методов, чтобы проверить, является ли запутанная петля реальным узлом или просто тривиальным узлом.
Райдемайстер движется
Движения Рейдемейстера — старейшая проверка того, является ли узел тривиальным. Это набор из трех разрешенных изменений узла для перевода его из одного состояния в другое. Последовательность этих ходов является доказательством того, что узел на самом деле является развязанным узлом.
На приведенной ниже диаграмме показано, как распутать узел Виновника с помощью движений Райдемайстера. 2 Обратите внимание, что первый шаг увеличивает количество пересечений, прежде чем его можно будет распутать.
Другими словами, если вы возьмете сложный узел с большим количеством пересечений и будете выполнять одно случайное движение Рейдемейстера в секунду, то поиск решения может занять гораздо больше времени, чем множество эпох Вселенной. Обратите внимание, что это непостижимо большое число является максимальным количеством случайных ходов. При наличии человеческого интеллекта большинство неувязок можно разрешить гораздо быстрее.
Алгоритмы развязывания
Ходы Райдемайстера — это наглядный и практичный способ распутать математические узлы. Но этот процесс требует некоторой человеческой проницательности и творчества. Математики задаются вопросом, как мы можем автоматически решить проблему развязывания узлов.
Вольфганг Хакен разработал алгоритм, позволяющий определить, является ли проекция узла неузлом. Однако его алгоритм настолько сложен, что никогда не был реализован.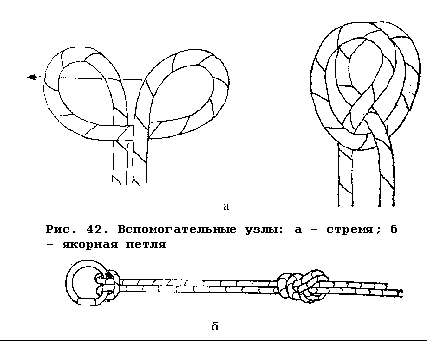
{C \log{n}}$ шагов, что меньше, чем несколько возрастов Вселенной.
В 1954 году Алан Тьюринг писал: «Пока не известен систематический метод, с помощью которого можно было бы определить, одинаковы ли два узла».
В 2021 году Марк Лакенби продемонстрировал выдающееся мастерство Гордиана, раскрывая новый алгоритм распознавания узлов, работающий за квазиполиномиальное времяhttps://t.co/0jGImTa9Uc pic.twitter.com/Y0n15Bu8DT @OxUniMaths) 2 февраля 2021 г.
Если вам интересно узнать о теории узлов, то я очень рекомендую лекцию Джессики Перселл по математике узлов из Школы математики Университета Монаша. Если вам нравится углубляться в теорию математических узлов, посмотрите увлекательные лекции Энтони Босмана в Университете Эндрюса.
Зал славы Unknot Diagram
Теоретики узлов, работающие над проблемой развязывания узлов, разработали несколько чертовски сложных тривиальных узлов для проверки своих догадок о проблеме развязывания узлов и своего программного обеспечения.
3
В то время как эти конструкции, безусловно, имеют математическое значение и играют роль в распутывании тайн вселенной, неузелок также может быть прекрасной вещью. Сложные узлы по своей сути обманчивы, потому что они не то, чем кажутся. Развязки — это замаскированные узлы, и попытка распутать их в уме может оказаться непростой задачей.
Гериц
Лебрехт Гериц был немецким математиком, который почти столетие назад сконструировал несколько тривиальных узлов. Его самый известный узел имеет одиннадцать пересечений. Прелесть этого узла в том, что вы можете увеличить количество перекрещиваний, добавляя клубки на левой и правой частях посередине.
Гёриц без узлов (11 скрещиваний). 4Тистлтуэйт
Морвен Тистлтуэйт — теоретик узлов, внесший существенный вклад в эту область. Он стал соавтором нотации Даукера-Тистлтуэйта, которая представляет собой инструмент для кодирования узлов для компьютеров. Он также определил тривиальный узел с пятнадцатью пересечениями, который часто цитируется в литературе.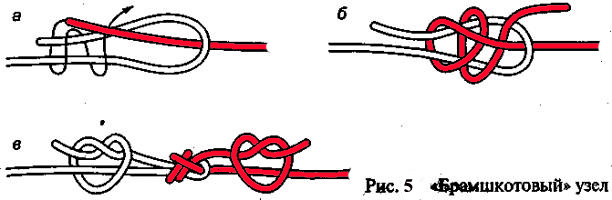
Очиай
Японский исследователь Мицуюки Очиаи разработал компьютерную программу для решения проблемы развязывания узлов. Он также построил четыре сложных тривиальных узла с увеличивающимся числом пересечений для проверки своих теорем и программного обеспечения. На изображении ниже показаны первые два его творения.
Первые два тривиальных узла Очиай (16 и 45 пересечений). 6Хакен
Вольфганг Хакен разработал самые сложные тривиальные узлы, доступные в литературе. Брайан Сандерсон привел пример того, как распутать творение Хакена.
Хакен известен тем, что совместно решил теорему о четырех цветах, которая гласит, что любую карту можно заполнить только цветами, чтобы никакие две соседние области не были одного цвета. Вы также можете применить эту теорему к его знаменитому узлу, показанному ниже.
Гордиев узел Хакена (141 пересечение). 7 Название этого узла связано с классической легендой о гордиевом узле.
Александру Македонскому было предложено развязать узел. Местная легенда гласила, что тот, кто сможет отменить это, будет править Азией. Вместо того, чтобы использовать приемы Райдемайстера или осторожно распутать веревку, он смело перерезал ее своим мечом.
Развязки в искусстве
Узлы были частью человеческой культуры на протяжении десятков тысяч лет. Люди раннего каменного века использовали узлы для создания рыболовных сетей и связывания вещей. Узлы не только практичны; они также фигурируют в искусстве. Мы находим изображения узлов в искусстве культур по всему миру и на протяжении веков. 8
Традиционные песочные рисунки Вануату, о которых я говорил в предыдущей статье, выглядят как геометрические проекции узлов. Большинство дизайнов рисуются пальцем на песке одной непрерывной линией. Поскольку палец не отрывается от песка, эти узоры представляют собой тривиальные узлы.
Схема рисунка на песке Ни-Вануату (изображение черепахи и батата). 9 Незавязанность вдохновляла не только математиков, но и художников-визуалистов.
Например, художник-абстракционист Джеймс Сиенна написал несколько работ, вдохновленных распутыванием. Будут ли эти конструкции на самом деле тривиальными узлами, еще неизвестно.
Мик Бертон — художник непрерывной линии, что означает, что он рисует картины одной непрерывной линией. Мик нашел вдохновение в теории узлов и, в частности, в гордиевом узле Хакена, благодаря которому была создана эта замечательная картина.
Мик Бертон, Скручивание, перекрывающаяся окраска гордиева узла Хакена.Волшебное развязывание
Волшебники любят использовать веревки и узлы, чтобы создать иллюзию волшебства. В архиве колдовства перечислены сотни эффектов, связанных с узлами. Большинство из них либо вызывают появление узлов, либо их растворение.
Распускающийся узел — это фокус, в котором фокусник вроде бы завязывает настоящий узел, но он тает. Эти типы трюков неразборчивы в движении. Фокусники разработали ряд техник, чтобы завязать узел.
В этом видео фокусника Дуга Конна показано, как завязывать два наиболее распространенных распускающихся узла.
Распутывание узлов обманчиво, потому что, по нашему опыту, каждая спутанная веревка завязана узлом. К сожалению, мы не можем определить, завязан ли узел на веревке, просто взглянув на него. Сложность проблемы развязывания узлов в математике поддерживает эту интуицию.
Так же, как математические узлы, растворяющиеся узлы названы в честь человека, который их составил. Двумя самыми известными вариантами являются узел Чефало и узел Охотничий лук, которым Дуг обучает в своем видео.
Магия и топология часто идут рука об руку, поскольку множество трюков используют топологию либо как метод, либо как сюжет. Известный теоретик узлов Луи Кауфман любит показывать на своих лекциях фокусы с узлами.
Итак, давайте относиться к этим двум растворяющимся узлам так же, как к математическим проекциям, которые мы видели выше.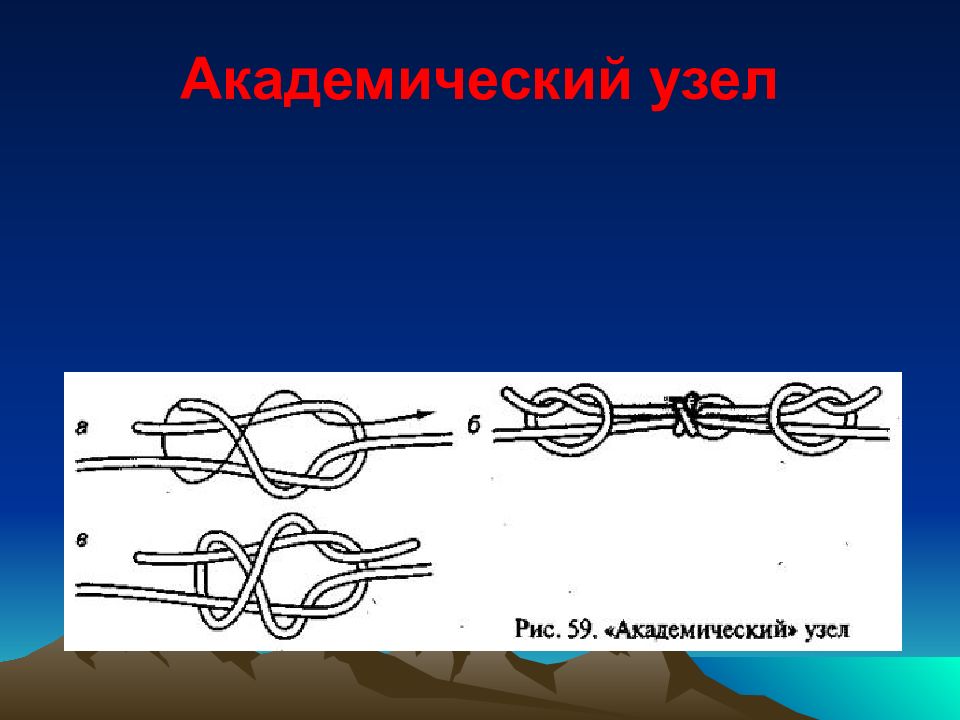
Сначала я сделала узлы, соединила концы и разложила их на столе, прежде чем распустить. Затем я сфотографировал веревки и нарисовал проекцию.
На полученных диаграммах показаны проекции узла Чефало (11 пересечений) и бантика Хантера (9 пересечений).переходы). Вы также можете комбинировать эти узлы, завязав узел Чефало поверх банта, что дает развязку с 20 пересечениями.
Возможно, математик, читающий эту страницу, сможет доказать, что это действительно тривиальные узлы, не дергая за концы.
Математическая проекция узла Чефало и банта Хантера.Ода развязному
Эта ода неизвестному показывает, что она отнюдь не тривиальна. Наоборот, за неувязкой скрывается глубокая математическая сложность, и она вдохновляла как художников, так и фокусников.
Сложные тривиальные узлы обманчивы, потому что они кажутся более сложными, чем они есть на самом деле. Так что в следующий раз, когда вы застрянете с запутанным садовым шлангом, не паникуйте, а найдите развязку, которая прячется внутри.
Возможно, более важный урок заключается в том, что как бы ни была запутана ваша жизнь, есть способ упростить ситуацию.
Не стесняйтесь обращаться ко мне или оставить комментарий ниже, если у вас есть какие-либо дополнения к моей коллекции unknots.
Примечания
1
Адамс, CC, Книга узлов: элементарное введение в математическую теорию узлов (1994), Нью-Йорк: WH Фриман.
2
Хенрих А. и Кауфман Л. Х., Unknotting Unknots, The American Mathematical Monthly , 121(5), 379 (2014) DOI 10.4169/amer.math.monthly.5.371.
3
Бертон, Б.А. и др. Жесткие диаграммы развязывания, (2021). архив: 2104.14076.
4
Кауфман, Л. Х., и Ламбропулу, С., Жесткие развязки и разрушающиеся клубки, Серия , посвященная узлам и всему , 187–247 (2011) DOI 10.
1142/9789814313001_0009.
5
Петронио, К., и Занеллати, А., Алгоритмическое упрощение диаграмм узлов: новые ходы и эксперименты (2016). архив: 1508.03226v3.
6
Очиаи, М., Нетривиальные проекции тривиального узла, Звездочка , 192, 7–10 (1990).
7
Стюарт, И., Кабинет математических редкостей профессора Стюарта (2008), Лондон: Profile Books.
8
Яблан С., Радович Л., Сазданович Р. и Зекович А., Узлы в искусстве, Symmetry , 4(2), 302–328 (2012) DOI 10.3390/ сим4020302.
9
Дикон, А. Б., и Веджвуд, С. Х., Геометрические рисунки с Малекулы и других островов Новых Гебридских островов, Журнал Королевского антропологического института Великобритании и Ирландии , 64, 129–175 (1934) DOI 10.
2307/2843952.
Поделитесь этим контентом
Насколько крепок ваш узел? | Новости Массачусетского технологического института
Известно, что в парусном спорте, скалолазании, строительстве и любой деятельности, требующей закрепления веревок, одни узлы прочнее других. Любой опытный моряк знает, например, что один тип узла прикрепит шкот к стакселю, а другой лучше прикрепит лодку к свае.
Но что именно делает один узел более прочным, чем другой, до сих пор не было понятно.
Математики и инженеры Массачусетского технологического института разработали математическую модель, которая предсказывает, насколько устойчив узел, основываясь на нескольких ключевых свойствах, включая количество задействованных пересечений и направление, в котором сегменты веревки скручиваются при затягивании узла.
«Эти тонкие различия между узлами критически определяют, является ли узел прочным или нет», — говорит Йорн Дункель, доцент математики Массачусетского технологического института. «С этой моделью вы сможете увидеть два почти идентичных узла и сможете сказать, какой из них лучше».
«Эмпирические знания, отточенные на протяжении веков, позволили выявить лучшие узлы», — добавляет Матиас Колле, доцент Rockwell International Career Development в Массачусетском технологическом институте. «И теперь модель показывает, почему».
Дункель, Колле и аспиранты Вишал Патил и Джозеф Сандт опубликовали сегодня свои результаты в журнале Science.
Цвет давления
В 2018 году группа Колле разработала эластичные волокна, которые меняют цвет в ответ на напряжение или давление. Исследователи показали, что когда они тянули за волокно, его оттенок менялся с одного цвета радуги на другой, особенно в областях, которые подвергались наибольшему стрессу или давлению.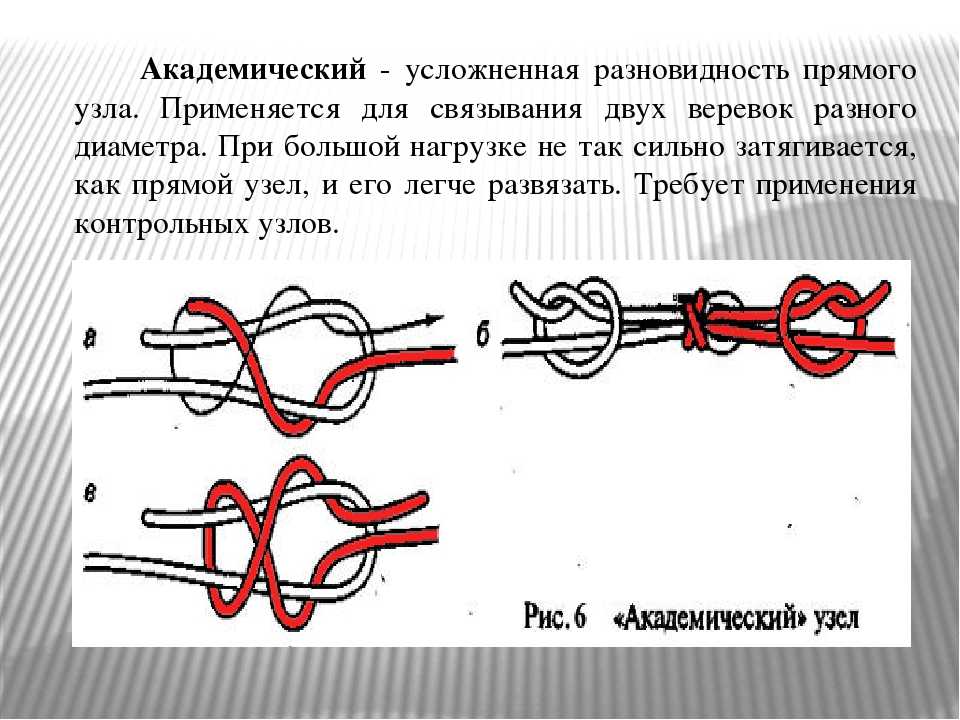
Пример прямых узлов.
Колле, доцент кафедры машиностроения, был приглашен математическим факультетом Массачусетского технологического института, чтобы выступить с докладом о волокнах. Дункель был в зале и начал обдумывать идею: что, если бы волокна, чувствительные к давлению, можно было бы использовать для изучения устойчивости узлов?
Математики уже давно заинтригованы узлами настолько, что физические узлы вдохновили целую область топологии, известную как теория узлов — изучение теоретических узлов, концы которых, в отличие от реальных узлов, соединены в непрерывный узор. В теории узлов математики стремятся описать узел в математических терминах, а также все способы, которыми его можно скрутить или деформировать, сохраняя при этом свою топологию или общую геометрию.
«В математической теории узлов вы отбрасываете все, что связано с механикой», — говорит Дункель. «Вас не волнует, жесткое у вас волокно или мягкое — с математической точки зрения это один и тот же узел.
Но мы хотели посмотреть, сможем ли мы добавить что-то к математическому моделированию узлов, учитывающее их механические свойства, чтобы иметь возможность сказать, почему один узел прочнее другого».
Спагетти-физика
Дункель и Колле объединились, чтобы определить, что определяет стабильность узла. Команда впервые использовала волокна Колле для завязывания различных узлов, в том числе узлов «трилистник» и «восьмерка» — конфигурации, которые были знакомы Колле, заядлому моряку, и членам группы Дункеля, занимающимся скалолазанием. Они сфотографировали каждое волокно, отметив, где и когда волокно изменило цвет, а также силу, которая была приложена к волокну, когда оно было туго натянуто.
Исследователи использовали данные этих экспериментов для калибровки модели, которую ранее применила группа Данкеля для описания другого типа волокон: спагетти. В этой модели Патил и Дункель описали поведение спагетти и других гибких, похожих на веревку структур, рассматривая каждую нить как цепочку маленьких дискретных, соединенных пружиной бусин.
То, как изгибается и деформируется каждая пружина, можно рассчитать на основе силы, приложенной к каждой отдельной пружине.
Ученик Колле Джозеф Сандт ранее составил цветовую карту на основе экспериментов с волокнами, которая коррелирует цвет волокна с заданным давлением, приложенным к этому волокну. Патил и Дункель включили эту цветовую карту в свою модель спагетти, а затем использовали модель для имитации тех же узлов, которые исследователи завязывали физически с помощью волокон. Когда они сравнили узлы в экспериментах с узлами в моделировании, они обнаружили, что цветовой узор в обоих случаях был практически одинаковым — признак того, что модель точно имитировала распределение напряжения в узлах.
Уверенный в своей модели, Патил затем смоделировал более сложные узлы, принимая во внимание, какие узлы испытывают большее давление и, следовательно, являются более прочными, чем другие узлы. После того, как они классифицировали узлы на основе их относительной прочности, Патил и Дункель стали искать объяснение, почему одни узлы прочнее других.
Для этого они составили простые схемы известных узлов «бабушка», «риф», «вор» и «горе», а также более сложные, такие как «каррик», «цеппелин» и «альпийская бабочка».
Пример рифового узла.
Каждая диаграмма узла изображает структуру двух нитей в узле до того, как он туго затянут. Исследователи включили направление каждого сегмента нити при ее вытягивании, а также место пересечения нитей. Они также отметили направление вращения каждого сегмента нити при затягивании узла.
Сравнивая схемы узлов различной прочности, исследователи смогли выявить общие «правила счета» или характеристики, определяющие устойчивость узла. По сути, узел прочнее, если в нем больше пересечений нитей, а также больше «крутильных колебаний» — изменений направления вращения от одного сегмента нити к другому.
Например, если сегмент волокна поворачивается влево на одном пересечении и поворачивается вправо на соседнем пересечении, когда узел затягивается туго, это создает колебание крутки и, таким образом, противодействующее трение, что повышает устойчивость узла.
Если, однако, отрезок вращается в одном и том же направлении на двух соседних пересечениях, колебания крутки отсутствуют, и прядь с большей вероятностью будет вращаться и проскальзывать, образуя более слабый узел.
Они также обнаружили, что узел можно сделать прочнее, если в нем будет больше «циркуляций», которые они определяют как область в узле, где две параллельные нити закручиваются друг против друга в противоположных направлениях, подобно круговому потоку.
Принимая во внимание эти простые правила подсчета, команда смогла объяснить, почему, например, рифовый узел прочнее бабушкиного узла. Хотя они почти идентичны, рифовый узел имеет большее количество колебаний крутки, что делает его более стабильной конфигурацией. Точно так же узел цеппелина из-за его немного более высокой циркуляции и колебаний крутки прочнее, хотя, возможно, его труднее развязать, чем альпийская бабочка — узел, который обычно используется в альпинизме.
«Если вы возьмете семейство похожих узлов, из которых эмпирические знания выделяют один как «лучший», теперь мы можем сказать, почему он может заслужить это отличие», — говорит Колле, предполагающий, что новую модель можно использовать для настройки узлов.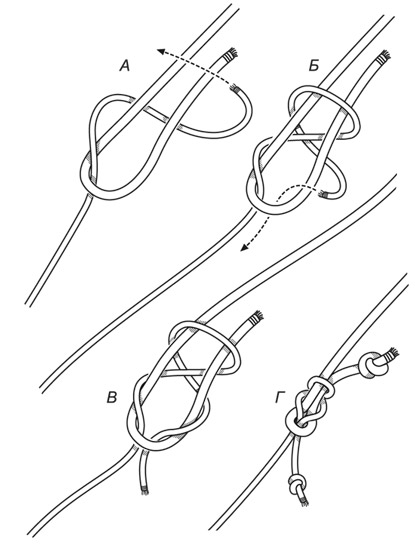
различной мощности для конкретных применений. «Мы можем играть узлами друг против друга для использования в наложении швов, плавании, альпинизме и строительстве. Это замечательно.»
Это исследование было частично поддержано Фондом Альфреда П. Слоана, Фондом Джеймса С. Макдоннелла, Центром инноваций в области травматологии Джиллиан Рени Степпинг Стронг при больнице Бригама и Женской больницы и Национальным научным фондом
Поделитесь этой новостной статьей:
Упоминания в прессе
Quanta Magazine
Quanta Magazine Репортер Девин Пауэлл рассказывает, как исследователи Массачусетского технологического института разработали новую модель, помогающую определить, почему одни узлы прочнее других. Исследователи надеются, что «результаты сыграют роль в разработке новых способов завязывания, петли, скручивания и иного формирования клубков из веревки, добавляя новое прогностическое измерение в теорию узлов».
Полная история через Quanta Magazine →
Smithsonian Magazine
Исследователи Массачусетского технологического института разработали модель, которая помогает разгадать тайну того, почему одни узлы более стабильны, чем другие, сообщает Тереза Мачемер для Smithsonian .
Исследователи «сопоставили математическую теорию узлов с изменяющим цвет волокном, разработанным в 2013 году», — объясняет Мачемер. «Поскольку волокно меняет цвет под давлением, исследователи смогли измерить физические свойства и добавить данные к своим вычислительным моделям узлов».
Полная история из Smithsonian Magazine →
Popular Mechanics
Группа исследователей Массачусетского технологического института использовала волокна, меняющие цвет, чтобы лучше понять узлы, сообщает Кэролайн Делберт для Popular Mechanics . Используя вычислительную модель, «команда Массачусетского технологического института могла бы гипотетически использовать свои исследования для создания совершенно новых узлов, максимально безопасных для человека», — объясняет Делберт.
Полная история через Popular Mechanics →
Scientific American
Репортер журнала Scientific American Джереми Хсу пишет, что исследователи Массачусетского технологического института использовали волокна, меняющие цвет, для разработки новой математической модели для прогнозирования стабильности узлов.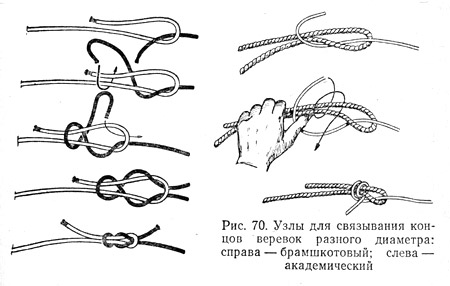
Ваш комментарий будет первым